Bitcoin is one of the most elegant and innovative solutions to emerge in the 21st century. The concept of decentralized bookkeeping - commonly referred to now as blockchain technology - that was first introduced by Bitcoin is such a powerful idea that it has spawned a $2 trillion cryptocurrency industry and spurred hundreds of thousands of the brightest minds in tech, finance, government, and many other fields to flock to work on it.
While there is a lot of noise made about the price, regulation, and politics of cryptocurrencies, there is comparatively little talk of the clever and ingenious mechanism that makes Bitcoin - and by extension many other blockchains - actually work. In this article, I attempt to explain the inner workings of the Bitcoin mechanism in such a way that non-technical curious readers can walk away with more conceptual understanding of the Bitcoin blockchain than many of the folks who even work in the crypto industry.
The world would be a much richer place if more people understood the fundamental ideas and creativity powering Bitcoin. Besides sharing with readers the sense of intellectual stimulation that comes with understanding a brilliant idea, I hope to also pique readers’ interest to dive deeper into this field. This topic has some personal significance to me because I previously started a company in and worked in this space, but that is a story for another time.
For now, all that remains is to dive in - while this article is slightly long, I promise readers who make it to the end that their effort will be worth it!
Disclaimers
Don’t be fooled into thinking I am an expert - I am just a seeker trying to learn, and I have a lot more to learn about Bitcoin/cryptocurrencies. I have intentionally misrepresented some elements of the Bitcoin mechanism to make it simpler, and I have altogether omitted many details as well.
I won’t go into too much technical detail, but it is impossible to truly get Bitcoin (or any cryptocurrency) without understanding some concepts from cryptography. So there will be some technical stuff (and budget homemade diagrams).
I won’t talk about the Bitcoin price, regulation, investment advice, geopolitical ramifications, or any of that other stuff. Some people have made interesting comparisons between Bitcoin’s creator and Martin Luther (the Protestant reformer who argued for the separation of church and state), but I am not talking about the separation of money and state, I am only focusing on the mechanism of how Bitcoin works. If you are intrigued by this post and want to learn more, I will leave a reading list at the end of the article, along with some FAQs.
Index
What Is Bitcoin And What Is Bitcoin’s Objective?
Trust In Numbers: The Cryptography That Makes Bitcoin Work
The Decentralized Architecture Of Bitcoin
Understanding A Bitcoin Transaction
A Deep Dive Into Bitcoin Mining
Understanding The Structure Of A Blockchain
FAQs
Glossary
1. What Is Bitcoin And What Is Bitcoin’s Objective?
Ok, before we even come to that question, let us ask:
What even is Bitcoin in the first place?
Bitcoin is many things. Firstly, it is a free to use, open-source computer program. Anybody can view this program’s code and begin using it. The computers running the Bitcoin program form a network. The network has certain rules, and its primary function is to enable people to make electronic payments. The currency used to make these payments is called bitcoin. When we refer to the Bitcoin program or the network, we typically use a capital B, and when referring to the currency, we use the small b - bitcoin.
So Bitcoin is many things - a program, a network, and a currency. In this article, we will be looking at how the rules of the program and network create viability for the currency. I think this is worth understanding because while we may take it for granted today, it is pretty crazy that Bitcoin even exists in the first place. The fact that I can use some computer program to reliably move money anywhere in the world without the permission, support, or interference of any government, bank, or payment network is frankly amazing. This becomes even more mind boggling when you consider that this system has grown entirely as a community-led initiative, with no real leadership or funding.
The history of this project is very interesting, but in this article we will only talk about the logic and intuition that gives the Bitcoin network its foundation. Everything that Bitcoin has achieved so far - its popularity, market capitalization, usage, and position as the technical and philosophical forefather to every other blockchain in the world - is built on this logical foundation. The system fundamentally makes sense, and its design is truly a thing of beauty. We will learn all about the design of the Bitcoin, but in order to understand how Bitcoin actually works, we first need to understand it’s objective.
Bitcoin was created in order to allow people to send and receive online payments without relying on any trusted financial institution or central intermediary of any kind.
There are lots of interesting economic and philosophical ideas around why this kind of objective is worth achieving:
If there is no central intermediary, there is no question of a corrupt central authority rigging the system in their own favour
If there is no central intermediary, the costs needed to sustain and trust that intermediary are removed from the transaction
If people are in custody of their own funds, everybody gains more security and financial sovereignty
In his 2009 white paper, Bitcoin’s mysterious and pseudonymous creator Satoshi Nakamoto puts forward some practical rationale for enabling decentralized Internet payments; amongst other things, he argues that if central intermediaries go away, their fees go away. Besides Satoshi, there are many other commentators who have provided powerful libertarian and economic justifications for Bitcoin. In this article, we will not spend any time thinking about these justifications for WHY we need a decentralized internet currency. All we need to know is that Bitcoin’s objective was to allow people to send and receive online payments without relying on any central intermediary.
So given this objective, the system has to satisfy the following criteria:
People need to be able to make and receive payments
There should not be any central third party or intermediary who people need to trust in order to use the payment system
The system should just ‘work’ well enough that it can serve as a viable payment system - if the payments made in this system can be fraudulent or prone to rollbacks or other critical errors, then nobody would trust it and the whole exercise of building the system would be futile
These are deceptively difficult conditions to satisfy, so let us see how Satoshi approached this problem through the Bitcoin system.
2. Trust In Numbers: The Cryptography That Makes Bitcoin Work
When you rely on a trusted institution to make payments, the logic goes something like this:
My money is held in an account managed by ABC Bank
I have a contract with ABC Bank that governs the rights and responsibilities around that money (they cannot lose it, cannot take it etc)
The contract is enforceable by law
The country I live in has the means and inclination to uphold the laws of the land
When you make a payment, you implicitly hold all these axioms to be true - you must trust the bank, the courts, and ultimately the state. Thankfully, our shared collective belief in things like justice and democracy have served us reasonably well so far, but the example above highlights just how much we need to rely on these pillars of trust in order to build systems of value.
If we want to build a system which is free of trust in a third party including even a legal system, how would we go about it? We would need some kind of utility that is equally accessible to all people. We would need this utility to behave in a manner that is predictable and demonstrably true, so that anybody could verify its assertions without relying on any third party or institution. Luckily for us, mathematics is perfect for this. Bitcoin moves the burden of trust from institutions to numbers; in particular, the Bitcoin protocol makes heavy use of cryptography. If we are to understand Bitcoin, we need to understand the following concepts from cryptography.
Hashing - The Most Important Concept in Bitcoin
All data inside computers is ultimately represented as binary digits called bits which can either be a 1 or a 0. The words in this article, the rules of the Substack server, and the program on your computer responsible for organizing all the colours and words on your screen can all ultimately be broken down into 1s and 0s. Don’t ask me how that is done - we humans have been able to invent some pretty crazy stuff using just electrical circuits. It regularly blows my mind.
Anyway, a hash function is a special kind of mathematical function that takes in some bits as an input and transforms those bits into a fixed length output. The act of performing a hash function on some data is called hashing. The output of a hash function is called a hash.
Thats so vague, what does the function do?
In simple terms, the hash function takes the input, breaks it up into equal bite sized packets, and repeatedly puts each of those packets through a jumbling process. In the jumbling, the bits of the input get mixed up and moved around so that they are totally different to the bits of the output (which unlike the input, is of a fixed length).
Before we illustrate the properties of hash functions using live examples, we might take a moment to study the desirable qualities of a good hash function.
Hiding: A good hash function hides the input. When you use a hash function to get an output, there should be no way that you can link or trace that output back to any input. If x is the input and H(x) is the output after hashing, there is no way that we should be able to determine x if we only have H(x). This is possible because hashing is a one-way process. Unlike adding and subtracting, the arithmetic operations involved in hashing are very difficult to undo. The act of hashing something is quick and easy, but the act of taking a hash and trying to reverse engineer the input is practically impossible. For comparison, you could think of mixing two different colours of sand - it is simple and quick to mix up the sand, but much harder and more time consuming to separate it into the original components. We might also add here that hashing is a deterministic process. That means hashing the same input will always give you the same output - there is no randomness involved in the jumbling, only complicated arithmetic that is very easy to do while generating a hash but impossible to do when trying to turn a hash back into its input.
Collision Resistant: This means that it should be hard to find two inputs that have the same output. Note: since the output of a hash function has a fixed length and the inputs can theoretically be infinite, there will always be some possible collisions, but it should be very hard to find two inputs x and y where H(x) = H(y). Another way you can think of this is that almost each and every input will have its own unique output.
Puzzle Friendliness (or Unpredictability): Imagine I want to find an output of a hash function where the first 7 bits are all 0s and there are no 1s. In a good hash function, this should be really hard to do. If there is some trick that will give you outputs that start with 0s, then the hash function is not puzzle friendly. In a puzzle friendly hash function, the best strategy for finding a given output should always be dumb trial and error. There are no shortcuts for finding a given output except to just keep trying different combinations of inputs and hoping you get lucky. Another way to look at this is unpredictability - before you hash an input, there is no way to tell what the output will be. You just have to hash it and see because you can’t predict the output.
Let's use some live examples to bring these concepts to life. To do that, we will generate hashes using this online hash calculator. As an input, we will enter a phrase in human-readable language. Behind the scenes, the computer will convert our phrase into its underlying binary representation and then feed all those 1s and 0s into a hash function called SHA-256.
The hash function will then jumble up all of the bits and produce a binary output. The computer will then take the binary string of 1s and 0s and turn it into language that you and I can read easily.
(Side Note: SHA-256, short for Secure Hashing Algorithm 256, is a hash function developed by the US National Security Agency in 2001. The function always spits out hashes of a fixed length of 256 bits. It is the hashing function used in Bitcoin, so we will stick with it in our examples).
Input Phrase: “Aaryaman is rueing the fact that he has embarked on a mission to write a detailed explanation of a complex topic. Not only is he concerned by the length of the piece, he is also worried about conveying difficult ideas with clarity.”
Output Hash: “4acf6fe00e54ae86dc57cdba8205e681139527a82676ec13e7c22a9fb18d4563”
Binary: If you are interested in seeing how the input and output are written in binary, you can simply copy and paste them into a binary encoder like this one
As you can see from the example above, the hash function has completely and unrecognisably changed the input. There is no way that we can look at that output and guess what the original form was. This is the ‘hiding’ property we discussed above.
While we cannot demonstrate the collision resistance of this hash function, you are welcome to try hashing some of your own inputs and seeing if you can get the same output. I can assure you that even if you hashed a billion different inputs, you would not get the same output twice. What we can do however, is make a slight change to the input and see what that does to the output.
Input Phrase: “Aaryaman is rueing the fact that he has embarked on a mission to write a detailed explanation of a complex topic. Not only is he concerned by the length of the piece, he is also worried about conveying difficult ideas with clarity!”
Output Hash: “27331c24ff6283d4d0051d13dd3a2090e0ca572133928e4802ac699ade91d475”
In this example, the only thing we did was turn the last character of the input from a full stop to an exclamation mark. Despite this minor change to the input, the output of the hash function has completely changed. It looks nothing like the output of the first input, and we had no way of predicting this new output barring just going ahead and hashing the input to see what happens.
This shows the puzzle friendliness or unpredictability of a hash function - with even the smallest change of 1 bit in the input, the output is changed in a completely unpredictable way. Taken together, these three properties of hash functions - hiding, collision resistance, and puzzle friendliness - actually make hashes a very useful tool in computer science.
Before we come to the way hashes are used in Bitcoin, let me share a few real world examples of hashing in action.
Password verification: When you sign up for any website, they (hopefully) never store your actual password as plain text in their database. They store a hash of your password instead. Every time you enter your password on a page, the website takes the characters you entered, hashes them, and compares the resulting hash with the hash stored in the website’s database. If the two hashes match, the website knows you are the real user and it logs you in. This way, if the website database ever gets hacked, the hackers will not get all of the passwords of the users, only the hashes of the passwords. And this is useless because if the hacker enters your password hash on a website, the website will just hash the characters he has put in and compare that with the hash of your actual password that it stored when you first created your password. Since the hash of the hash of your password is not the same as the hash of your password, these two values will not match and the hacker won’t be able to log in to your account. Plus, it is impossible for the hacker to turn your password hash back into the input, so he would have no way of doing anything useful with the hash of your password.
Checking the integrity of data: Imagine we are negotiating a 200 page legal agreement with a counterparty. The agreement is very complex and the placement of each comma and full stop is of extreme importance. Imagine that the final draft of this agreement is negotiated at 5am and needs to be printed and signed at 9am.
After preparing the final draft on Microsoft word on your own computer, you need to send it to the counterparty’s office to get printed. How can you be sure that at 9am the counterparty doesn’t change something before printing the agreement? It is not feasible to manually reread the agreement and check everything again. A better solution would be to hash the final draft after both parties agree. In this way, the 200 page document could be summarized into short but specific alphanumeric hash output like we saw before.
Before printing the final version at the counterparty’s office, the document could be hashed again. If there has been no change in the document, the output of the hash will be exactly the same. However, if there has been the slightest change in the input, the output hash would be totally incongruent with the first hash and it would be clear that the document has been tampered with and needs to be checked again.
This concept of using hashes to check the integrity of data is widespread in computer science, and indeed in Bitcoin. Even though it is impossible to turn a short 256-bit hash output back into the 200 page document to see WHAT has changed in the input, it is still very useful to compare the hashes of two files to see WHETHER something has been changed. This concept is used extensively when downloading software from the internet - the makers of the software share a hash of the software file called a ‘checksum’. The user of the software is supposed to hash the software file post-download and compare it with the checksum to ensure that nothing has been tampered with and he has not unknowingly downloaded some malware along with the software.
To tie up this section on the most important concept in Bitcoin, I leave you with this diagram that describes hashing.
Digital Signatures - The Second Key Concept in Bitcoin
The next and final cryptography concept we need to understand is digital signatures.
As a starting point, we need to know that cryptographers have discovered a category of numbers that have really unique properties. These numbers are special because they come in pairs, known as a ‘keypair’. One of these numbers is called a ‘private key’ and the other is called the ‘public key’. These numbers are called ‘keys’ because they hold the power to unlocking each other’s secrets.
Anybody can independently derive a unique keypair by using some special algebra. All the keypairs derived using the correct algebra will be able to sign messages and verify signatures.
Signing messages: As the name suggests, signing a message in cryptography is analogous to putting a special stamp or seal on an envelope.
In order to sign a message, you need to have a message and a private key. The message could be any data, just like the phrases we hashed earlier. The private key could be any private key that was correctly derived using the requisite cryptographical algebra. When you put the message and the private key into a special equation called a signing function, it is possible to get an output called a signature.
Inputs: Message, Private Key -----> Signing Function -------> Output: Signature
The signature basically looks like gibberish similar to the hashes we saw in the previous section.
Verifying signatures: Verifying a signature allows you to check whether a given signature was actually created by the right person.
If signing allows you to put a unique stamp on a message, verifying a signature allows you to check whether the stamp actually belongs to the purported owner of that stamp. In order to verify a signature, you need a message, a signature, and a public key. The public key should correspond to the private key used to generate the signature.
Inputs: Message, Signature, Public Key ----> Signature Verification Function ---> Output: True/False
The output of a signature verification function will tell you whether the given signature was really generated by signing the given message with the private key corresponding to the given public key. This answer comes in a true or false form.
Perhaps this concept can be better expressed through an example. Imagine that an army is planning a campaign. During the campaign, the generals of the army will be spread out in enemy territory and will be forced to communicate using messengers and couriers who could be intercepted. It is crucial that the generals are able to coordinate their movements, so before they spread out and go their separate ways, each of them independently generates a keypair.
The generals share their public keys with one another, but they keep their private keys to themselves. After exchanging public keys, the generals spread out in enemy territory and begin making plans.
Imagine that a courier comes to one of the generals with an urgent letter from a fellow general warning of an imminent ambush by local rebels. Should the general believe the letter? The news in the letter might be made up by the enemy to distract the general and his army from their true objective. If that were the case, trusting the letter would have terrible consequences. However, if the letter is indeed true, then not trusting it would have terrible consequences too.
Luckily for our friend the general, he doesn’t need to trust the courier or the letter. Supposing the message came accompanied by a digital signature, our general has all of the tools he needs to verify the signature for himself without trusting anybody else. The contents of the letter would be the message, the signature would be some alphanumerals that would be sent along with the letter, and the public key required for verifying the signature would be the public key of the purported sender of the letter.
Since our general has the message, has the signature, and knows the public key of all the other generals, he can just put all of this into a signature verification function and see whether the letter was really signed by one of his peers or was fabricated. This is really useful for ensuring secure and reliable communications - and this is exactly why digital signatures are used extensively throughout the Internet. In fact, digital signatures are working in your browser at this very moment. If you look at the URL bar of your browser, you will probably see a lock icon next to the substack.com address. This lock bar appears because your browser is telling you that the data you see on the screen has actually been sent by substack.com and not somebody else pretending to be them!
You see, each website effectively has its own legal public key. When your browser shows you the lock icon, it is telling you that you are communicating with a party can that prove they own the corresponding private key - ie. the signatures generated by substack.com match the public key that substack has listed with the government!
To wrap up the section on digital signatures, it's worth quickly running over the properties of good digital signature schemes:
Verifiability: You must be able to verify a signature for a given private key if you are given the message, the signature, and the corresponding public key
Unforgeability: Using just the public key, it should be almost impossible to generate a valid signature. Even if a hacker has seen a million signatures generated by a given private key, he should still not be able to forge signatures that can fool people into thinking he knows the private key.
3. The Decentralized Architecture Of Bitcoin
Congratulations! You made it through the most technical section of this blog and you are now able to understand seminally important concepts in cryptography!
All of you get to look at this image of a nerd dog as a reward!
Now, coming back to the topic at hand, let us take a second to remind ourselves of Bitcoin’s objective: to enable people to make online payments without relying on any trusted intermediary.
In the case of a central intermediary, how do payments work? Probably something like this:
As we can see here, the central intermediary in this system is the bank. In addition to providing a central server, the bank also maintains its own ledger.
When User A wishes to send $100 to user B, he goes to the bank’s website (hosted on the bank’s server) and clicks the buttons required to log in and make a transfer. If this goes smoothly and the bank is satisfied that A has the appropriate credentials and balance to make this payment, the bank will update the ledger to reduce A’s balance by $100 (plus some fees maybe) and increase B’s balance by $100.
This is pretty straightforward, and works pretty well for most use cases. But if you need to make a payment system with no central intermediary, how would you do it? Let us look at Satoshi’s approach.
Satoshi, the maverick, gave every single user their own individual ledger! You might have noticed that we also gave every user their own name. The usual nomenclature of A, B, C or Alice, Bob etc. is too boring, so we spiced things up.
But what does it mean that Satoshi gave everybody their own ledger? Where does this ledger exist? Which server or computer is it stored on?
Bitcoin is a free, open-source (meaning anybody can read the code) computer program invented by Satoshi Nakamoto. Anybody can download the program and run it on their computers. There are different versions of the program, but they all do more or less the same thing - kind of how you can download Skype for Windows or Mac but they can still be used to talk to your friends in the same way regardless of which versions your friends are using.
So all the users now have the Bitcoin program running on their computers - there is no central server of any kind, just many individual computers which each have the same program. This is why Bitcoin is said to have a decentralized architecture.
Any computer running the Bitcoin program is called a node. So instead of having one central bank server, we now have four individual Bitcoin nodes run by Abdullah, Beelzebub, Celestine, and Dharmesh. Compared to the bank users, these folks have way more personality, as you can tell from their names.
Each of these nodes also has its own associated ledger which it maintains independently. We have now totally removed the central intermediary, since there is no longer a central server nor a central ledger! But we haven’t succeeded yet, we still need to tackle the problem of consensus: how can we ensure that each ledger in this system is consistent with the others?
In Bitcoin, maintaining consensus amongst all of the nodes is one of the biggest problems en route to achieving the objective. Specifically, the nodes need to all agree on a single, specific version of the ledger. There is no point if everybody has ledgers with different values - nobody will trust the system and it will be useless for payments.
In the centrally held bank ledger, the bank is the one who works to prevent fraud, double spending, rollbacks, and to generally maintain correct account balances across the system. In the absence of a central intermediary like a bank, who will do the work to ensure that transactions are valid and are recorded properly? How and why will everybody ensure that their ledgers are all consistent?
In the coming sections, we will see how Satoshi used cryptography and game theory to solve this problem. We will begin by looking at how transactions are made in Bitcoin.
4. Understanding A Bitcoin Transaction
Prior to understanding how the ledgers in the Bitcoin network achieve consistency, lets look at the units that comprise the ledger - transactions. In Bitcoin, transactions get added to the ledgers once every ten minutes on average. But these transactions don’t get directly added to ledger - they are first batched into groups of transactions called ‘blocks’.
Take a quick look at the simplified structure of a transaction in Bitcoin :
Sender: This is basically the public key of the sender
Recipient: This is basically the public key of the recipient
Amount: This is the amount of bitcoin to be sent
Mining Fee: We will explain this fee in a minute
Signature: This is the result of putting the first four fields in a signing function along with the sender’s private key
If you understood the concept of digital signatures, this structure should be pretty straightforward. Even if the concept is hazy, don’t worry because we will explain it again using emails as an analogy. So now that we know the structure of a bitcoin transaction, lets see how the transaction makes its way onto the ledgers of all of the nodes in Bitcoin network.
The first thing that happens is that Abdullah decides he wants to pay somebody, let us say Celestine.
Using the Bitcoin program - either directly on his own computer or through the hundreds of apps or websites that run the Bitcoin program on behalf of users - Abdullah can create a transaction that looks like this:
Sender: [Abdullah’s Public Key]
Recipient: [Celestine’s Public Key]
Amount: 0.05 bitcoin
Fee: 0.00002 bitcoin
Signature: 0014e4ef8402f36c7aa342efa7174ed1c9d399ae1c4a (when you sign the above information using a private key - in this case Abdullah’s private key - the signature looks something like this)
Ok so Abdullah has created this transaction but now he needs to make sure that this transaction is included in everybody’s copy of the ledger. So Abdullah ‘broadcasts’ his signature out to the network.
Presumably, some of you have used Bittorrent, Limewire, or some other p2p file sharing system. You know how your file sharing client can automatically discover other ‘seeders’ and ‘leechers’ and get files from them? Imagine your Bitcoin program can also connect with all the other computers running the Bitcoin program just like that.
So Abdullah has made his transaction (which we will now abbreviate to ‘tx’) and he has broadcast the tx to everybody else. The first thing that everybody else does when they get this tx from Abdullah is to check whether it is valid.
Is all the necessary information included here? Does it have a sender and receiver? Are the sender and receiver public keys in the proper format? This is easy to verify, each public key has a particular structure which is easy to verify, just like checking if an email address has an ‘@’ and a ‘.com’
Does the sender have the amount in his Bitcoin balance? Obviously, Abdullah should not be able to spend bitcoin he doesn’t own. In Bitcoin, all the nodes have their own independent copy of the entire ledger. So everybody should be able to easily check their own ledgers and calculate whether Abdullah can afford to make the transaction. To continue the email address analogy, imagine Abdullah’s public key is like his email address. Throughout the entire ledger, there are transactions going to and from this particular email address, so everyone can just check their internal ledger to see the final balance against Abdullah’s email address.
Is the transaction properly signed? To continue the email analogy, the signature allows all the nodes to check that Abdullah has properly authorized the transaction using his specific password. Using the signature, every node can see whether each exact detail in the transaction was properly authorized or not. If the signature doesn’t add up, the nodes will know that Abdullah didn’t actually authorize the transaction and that they should discard it from their mempool.
This is how Bitcoin uses digital signatures - anybody can independently generate a valid keypair and use the public key like an email address. You can share that email address with anybody, and they can use it to send bitcoin to that address.
However, in order to spend bitcoin, somebody who claims to own a certain email address or public key has to prove that they are in fact the rightful owner of the funds associated with that address. They are able to do this in an objective, easily verifiable way by entering their password for the email address - they sign the transaction with their private key.
If Abdullah’s transaction doesn’t meet any of the 3 validity criteria listed above, then the nodes who receive it will just throw it in the junk and forget about it. However, if this transaction meets all of these criteria, then it is considered valid, and the node receiving it will put it into a special bucket of valid transactions called the memory pool (or mempool).
So at this stage, Abdullah’s transaction has gone out to all the other nodes running the Bitcoin program. Each node has independently verified the transaction to check if it is valid. Upon finding that it is valid, each node has now put the transaction in its own individual mempool bucket.
Side note: In reality, not every transaction is received by every node. Due to bad internet for example, the connection between Abdullah and Dharmesh could be down. Therefore, Dharmesh’s mempool may not have this particular transaction. So in reality, each node’s individual mempool could be different from their peers - but for this post, let us assume they are all the same.
OK! So this is an encouraging milestone - Abdullah’s transaction is now in each node’s individual mempool. We are beginning to get some consistency amongst the nodes, but we are not there yet. This transaction is not yet confirmed - which means that it is not yet in the ledgers. It is only in the mempool waiting to go in the ledgers!
5. A Deep Dive Into Bitcoin Mining
In Bitcoin, the ledger is sacrosanct. This is the same for any payment system, even a centralized bank-run one. It is important to be very careful about what you put in the ledger because correcting mistakes can be very costly and painful.
This is doubly true for a decentralized payment system in which no central party can just pause the ledger and edit it to fix errors. In a decentralized system, every party has to agree on every tiny detail for the system to have consistency. For this reason, there is a lot of work which needs to go into creating new ledger entries in Bitcoin.
If all of this work was done for each and every transaction, it would be a nightmare. Therefore, Bitcoin groups transactions into ‘blocks’. Each block contains ~2000 transactions, and ledger entries are always made one block at a time. In this way, all the work and preparation that needs to be done to ensure a proper ledger entry can be amortized across all of the transactions in a block.
So how exactly does a block get added to the ledger?
Through a special process called mining Bitcoin. To understand mining, let us go back to where we left off with Abdullah’s transaction. Currently, Abdullah’s transaction is lying in the mempool bucket of each node.
Similar to how they received Abdullah’s transaction, each node might also have built up a mempool of hundreds or thousands of other transactions. All of these transactions are unconfirmed - they are valid transactions which everybody can independently verify, but they aren’t inside the ledger yet.
As we know, transactions need to go into a block to make it onto the ledger. In the Bitcoin program, blocks have a limited amount of space, which is why there are normally only around ~2000 transactions per block. There are usually always many more transactions lying in the mempool than there are free transaction slots in the next block. So how do nodes decide which transactions to put in the block?
Sender: [Abdullah’s Public Key]
Recipient: [Celestine’s Public Key]
Amount: 0.05 bitcoin
Fee: 0.00002 bitcoin
Signature: 0014e4ef8402f36c7aa342efa7174ed1c9d399ae1c4a (when you sign the above information using a private key - in this case Abdullah’s private key - the signature looks something like this)
If you look at the structure of a bitcoin transaction we had plotted, you can see that there is a mining fee associated with each transaction. This means that the sender of a transaction has set aside some fee that he is willing to pay to the miner for his transaction to get through onto the ledger.
But hold up - who is a miner?
The answer is any Bitcoin node that is working to try and add transactions to the ledger is a miner. Before we talk about how mining actually works, it is important to understand the incentives behind mining.
Why would these miners choose to build upon the ledger? Especially if it meant spending expensive computer power crunching all these numbers trying to verify signatures and validate transactions?
Well, one answer is the mining fees.
The mining fee, as we were just saying, is a voluntary amount that the sender of a transaction sets aside to give to a miner. Indeed, some people who create bitcoin transactions could choose to set the mining fee for their transaction as 0. And that’s fine, their transaction would still be valid and go into each miner’s individual memory pool.
Having said that, since the number of transactions in a block is limited, and there are always extra transactions lying around in the memory pool, the rational thing that any profit-maximizing miner would do is first try to process all the transactions with the highest mining fees.
But hold on a second - which one of the several independent nodes/miners gets to decide which transactions go into a block? Who gets the mining fee? Is it just equally split between all miners or is there some other system in place?
The answer is this - the person who decides which transactions go into a block is determined by a lottery-like process called the mining puzzle. This is an objectively verifiable hashing exercise that anybody can attempt to solve. The first person who solves the mining puzzle is entitled to decide which transactions go into the next block in the ledger. This lucky miner is also entitled to take the mining fees from all transactions within that block. Logically, each miner would therefore try to include the most lucrative high-fee transactions in their solutions to the mining puzzle.
So what we have here is a situation in which each miner is independently and selfishly trying to add the next block to the ledger. This block of transactions - that each miner is composing from the mempool and trying to add to the ledger - is called the miner’s candidate block. It is one of the several ‘candidates’ vying to be the next block in the ledger. Each block may have different transactions inside it - that depends completely on each miner, but as we established, most miners prioritize the transactions with the highest fees. I say miners are ‘trying’ to add a block to the ledger because solving the mining puzzle is a very difficult process.
The reason we need this process is because if each miner just independently added their own candidate blocks to the ledger, we would have thousands of disparate copies of the ledger floating around. Nobody would agree on what the real version of the ledger is, so nobody would accept bitcoin transactions and the payment system would be a failure. To get around this problem, Bitcoin has a mining puzzle that determines which specific miner gets to add which specific block of transactions to the ledger.
As a recap, we just learned that miners have to solve a puzzle in order to add blocks to the ledger. We also learned that one of the incentives for miners to solve this puzzle comes in the form of mining fees. In the next section, we will learn how exactly this mining puzzle gets solved and why this process helps Bitcoin create a decentralized payment system.
Solving the Mining Puzzle
Let us return to the example of Abdullah, Beelzebub, Celestine, and Dharmesh.
At this point in our example, Abullah’s transaction has made it into each miner’s mempool. Presently, each miner is composing a candidate block and is trying to add that block to the ledger by solving the mining puzzle.
Before we get into the actual mechanics of the mining puzzle itself, there is another important point you should know about the incentives for miners. Over and above the miner fees, there is another critical benefit for mining a Bitcoin block. That benefit is called the block reward - essentially, every time a new block is mined, the miner who solved the puzzle for that particular block gets 6.25 newly created bitcoin (worth $62,500 at the time of writing).
I say ‘newly created’ because these bitcoin literally come into existence for the first time. As a free, open source program, Bitcoin has some rules which everybody can see. One of these rules is that every time a mining puzzle is solved, the miner who successfully solved the puzzle can basically mint brand new bitcoin into existence, and every other node and miner has to record this minting transaction in their own copies of the ledger.
This block reward, along with the mining fees, is the main incentive to mine bitcoin in the first place. Anybody can claim these new bitcoin, as long as they are able to solve the mining puzzle. There is no way to generate ‘new’ bitcoin (as opposed to buying somebody’s existing bitcoin through a cryptocurrency exchange) except via mining.
When Satoshi started Bitcoin in 2009, he was the only miner on the network (naturally). Over time, as the idea started to take off, more and more people started mining. So even though Satoshi created the program, it is important to note that the means of generating bitcoin has always been the same - mining. Not even Satoshi is able to bestow himself new bitcoin because the program doesn't have any other means of creating bitcoin besides mining.
Anyway, there is one last thing you should know about the block reward before we come to the mining puzzle. The block reward keeps decreasing over time until it asymptotically tends to 0 when it approaches 21 million bitcoin in circulation. This means that the total number of bitcoin in the world cannot exceed 21 million (side note: while the number of 21 million may be low for a currency, each bitcoin can be divided into units of size 0.00000001).
Source: https://medium.com/@PhillipNunn/the-bitcoin-supply-curve-513554e6588d
When Satoshi designed the program, he wanted the supply of bitcoin to be capped so that the risk of inflation and debasement did not ruin the value of the currency. He wanted bitcoin to be scarce by design, so that the price would go up as the supply of new bitcoin kept slowing down to zero. This is one key reason why people think Bitcoin has value - it is a scarce resource with a fixed supply graph.
When the Bitcoin program was launched in 2009, each block reward gave miners 50 newly minted bitcoin. After 210,000 blocks had been added to the ledger (which took around 4 years), the block reward dropped to 25 bitcoin. After the next 210,000 blocks , it dropped to 12.5 bitcoin. Currently, the number of new bitcoin created in each block is 6.25. In 3-4 years, when the next 210,000 blocks are mined, that figure will halve again. By the time the supply of new bitcoin reaches 0, Satoshi intended for the mining fees in the transactions to compensate the miners for the loss of the block reward. The hope is that by then, the fees themselves will be valuable enough to sustain the cost of mining.
Apologies for that little digression, but we had to establish why exactly miners are trying to solve this puzzle anyway - we know the answer now: miners are incentivized to solve the mining puzzle because if they do so, they get a block reward of 6.25 newly minted bitcoin and they also get to claim all fees embedded in the transactions in the block they just created.
So how exactly do they solve the mining puzzle and create a block?
Let us go back to our last diagram and take a closer look at the structure of each candidate block.
There are some details here that were missing in the previous diagram because I just didn’t have the space to include them, but here is the basic structure of a Bitcoin block.
There are two things included in a Bitcoin block. The first thing is a bunch of transactions. As we saw earlier, each miner is free to include whatever transactions they want in their candidate block. There is a space constraint, but each miner can choose whichever transactions they wish to include in that space. As a refresher, each transaction basically has some fields like Sender’s public key, Recipient’s public key, Amount, Mining Fee, and Signature. Any node or miner can independently gauge the validity of a transaction by verifying the signature and checking that the sender of the transaction has enough balance in his account on the ledger.
Besides the transactions themselves, there is also another structure called the block header. The block header is just a list of a few things:
The Block Height
The Previous Block Hash
Transactions Hash
Timestamp
Difficulty
Nonce
We will cover each of these things, but will spend the most time on the difficulty as this is really at the heart of bitcoin mining.
Difficulty: If you remember our primer on hashing, you would know that a hash takes in some bits as an input, and spits out some bits as an output. A bit, as we know, is a 1 or a 0.
If we hash the following phrase in our SHA-256 hash generator, we get the following output:
Phrase (input): “shit i am scared I am losing my audience if I haven’t already lost them but we are almost at the end and I hope this can make sense to at least one person”
Hash (output): f331b6895c908a27178067ec0f43abf963d9a0a0477e96b4d5c56e1887f91bb1
Remember, while the input and output are both written in human readable characters, they are actually represented in binary bits. So here is a look at the first 10 bits of the output after converting it to binary:
01100110 00
In the first 10 bits of the hash of our phrase, there are 4 1s and 6 0s. Lets take a moment here to remember that hash functions have a property called puzzle-friendliness, which basically means unpredictability. It is very difficult to predict what the output hash of a given input will be without just going ahead and hashing it. What this effectively means is that when you hash something, each bit has a 50% chance of being a 1 or being a 0.
In our limited set of 10 bits, we had 60% 0s and 40% 1s. This is not too far from 50-50. If we took a larger number of bits, we would probably be even closer to 50-50 as the laws of probability would kick in.
Now, what if we asked what is the probability that the hash of a given phrase begins with the first bit as a 0? You would rightly say that the odds would be 50%. If I said what are the odds the first two bits are 0s, the probability would be 50% (½) * 50% (½), or 25%. The chances that the first three bits are 0s would be (½) * (½) * (½) or 12.5%.
As we can see, the probability of a given hash beginning with a certain number of 0s becomes exponentially lower the more zeros we add. If we want to get a hash that begins with ten 0s, the probability would be 0.098%.
In Bitcoin, the difficulty number tells us how many leading 0s we need in the hash of the block header for that block to successfully solve the mining puzzle. The higher the difficulty, the harder it is to solve the mining puzzle.
In the case of Abdullah’s bitcoin block above, the difficulty number is 10. This means that when a miner takes all of the fields in the block header and loads them all up into the SHA-256 hash function, he needs to get a resulting hash that starts with 10 zeros in order to satisfy the difficulty level and solve the mining puzzle. As we now know, there is only a 0.098% chance that the hash generated by a miner can satisfy the difficulty criteria.
This is obviously a really low number, but before we go any further, lets just unpack the sentence in bold above. The hash of the block header? What is that exactly? Well, all the fields we just listed in the block header are batched together, put into the SHA-256 hash function, and turned into a hash.
OK, but you didn’t even go into the different fields in the block header, only the difficulty?
Yes! So now is a great time to briefly explain the other fields in the block header, before we come back to the difficulty concept and wrap everything up.
Block Height: In Bitcoin, each block has a particular vertical ‘height’ depending on when it was inserted into the ledger. The first Bitcoin block, which was mined by Satoshi, is called the ‘genesis block’ and has a Block Height of 0. The next block which came after that has a Block Height of 1. The next one has a Block Height of 2, and so on. At the time of writing, the latest Bitcoin Block Height is 647360.
Time Stamp: This is the date and time at which the miner claims to have created the block
Transactions Hash: In simplified terms, the transaction hash is a hash of all of the transactions in a given bitcoin block. So when Abdullah is composing his candidate block, he will take the transactions he wishes to include from his mempool, organize them in a special order, and hash them all together so that they can be represented in a nice short single hash in the block header. The benefit of doing this is that you can very quickly compare two sets of transactions by computing their transaction hashes. If the two hashes are equal, then the two sets of transactions are identical. However, if I generate a different transaction hash from you, I would know that the transactions in our blocks are not the same. In the current example, the transaction hash for Block Height 20 is xyz
Difficulty: We just explained this above. For the current example, the difficulty is 10. This means that in order to solve the mining puzzle at this level of difficulty, the miners need to generate a block header hash that begins with 10 consecutive 0s. The odds of this happening on the first attempt are 0.098%. (If you want to know how the difficulty level of a block is set, this question is answered in the bonus FAQs at the end of the piece)
Nonce: As we saw above, the odds of a miner generating a solution to the mining puzzle on the first attempt are just 0.098%. So what should they do if they fail? Should they give up?
Not quite - because of the properties of hash functions, if you just change one thing in the input of a hash, the output will totally change. So if a miner tries to solve the puzzle and fails, they can take another crack at the mining puzzle by changing the nonce in their candidate block header and hashing it again. The miners change the nonce when attempting a new solution to the mining puzzle because the other fields in the block header are either fixed (such as the block height) or time-consuming to compute (the transaction hash). In contrast, the nonce exists solely for the purpose of helping miners come up with different solutions to the mining puzzle.
If you start with the nonce as 0, and keep increasing the nonce by 1 for every attempt, you can quickly generate many possible solutions to the mining puzzle. Since the output of a hash is unpredictable, each of these hashes of the block header with a different nonce will have an equal probability of yielding a block header hash which satisfies the difficulty criteria. There will always be some nonce value that makes a miner’s individual candidate block achieve the right number of 0s to solve the difficulty. This magic nonce number is what all miners are searching for!
In our particular case, the difficulty was 10 which means that the odds of generating a block header hash with the correct difficulty level is 0.098%. On average, a miner would need to make about 1020 different block header hashes before stumbling upon one which begins with 10 zeros. In Abdullah’s candidate block, the nonce is 26. So that means that if you include the number 26 with all the other fields in the block header and hash them, the output hash has ten leading 0s. Judging by the nonce, it took Abdullah 26 tries to get the right combination of fields to arrive at a block header hash which matches the difficulty required by the mining puzzle. So he is a lucky guy!
But luck will not always be on the side of miners - at its core, the chances of a Bitcoin miner successfully solving the mining puzzle are directly correlated with how many hashes that miner can perform in a second. Lets say that Abdullah can perform 1020 hashes per second on his computer but Dharmesh can only perform 100 hashes per second, Abdullah would be much more likely to find the solution to the mining puzzle before Dharmesh.
For this reason, the main criteria for determining your success as a Bitcoin miner is your hash power - how many hashes can you perform in a second? The higher your hash power, the better your chances of finding the solution to the mining puzzle. When Bitcoin was first launched, it was feasible to use a laptop for mining because the collective hash power of all the miners using the program was low. Today, however, miners use specialized computers that are designed specifically to optimize the speed of hashing block headers.
Modern Bitcoin mining rigs consisting of specialized computers
Today, Bitcoin miners have optimized their chances of mining blocks using different strategies, ranging from choosing places with low energy costs, to trying to design the most efficient mining chips, to crowdsourcing computing power into aggregations called mining pools.
In a single second, the collective number of hashes that all the computers in the Bitcoin network can currently generate is 140 exahashes, which can be written as:
140,000,000,000,000,000,000
This is what Bitcoin articles mean when they say that Bitcoin mining involves solving some mathematical problems. Billions of dollars worth of computers are racing to find a hash for the next block which begins with an improbably high number of leading zeros. Each computer is trying to generate the one lucky hash out of quintillions of hashes that happens to begin with a large number of zeros. This is how hashes are used in Bitcoin’s mining puzzle.
If you are reading this and things are still not making complete sense, don’t despair. These are complex concepts to assimilate (or to explain, and I am sure I am sucking at that right now). There are still one or two key concepts we haven’t explored, but we cover everything in the next and final chapter!
6. Understanding The Structure Of A Blockchain
By the end of this piece, everything will hopefully come together, but you need to have a little patience as we first need to understand the last piece of the block header, the previous block hash.
Previous Block Hash: In Bitcoin, the blocks are organized sequentially so that each block header includes the hash of the block header of the previous block that came before it. Take a look at this diagram.
Firstly, let us assume that the candidate block that Abdullah was trying to mine at Block Height 20 got confirmed. This basically means that Abdullah solved the mining puzzle and sent his candidate block to all the other miners. Upon receiving Abdullah’s block, each miner independently checked to make sure it was valid.
To do this, they first hashed all the transactions he sent in his candidate block and independently computed his block’s transaction hash for themselves. If that checked out, then they checked the other values in Abdullah’s candidate block header and if they all looked OK, they hashed the values to generate Abdullah’s candidate block header hash. Upon doing that, they could easily check the number of 0s in the hash to see whether it really hit the difficulty target. Remember, performing a hash is easy to do - so checking that the hash value was correct was extremely quick, even though generating the right hash value for Abdullah and the other miners was very unpredictable and hard. Anyway, when each miner verifies for themselves that the hash value is correct, they append Abdullah’s block to their local copy of the ledger.
When they append this block of transactions to their ledgers, they confirm all the transactions Abdullah elected to include in his block. All of those transactions are inside the ledger now! Crucially, Abdullah would have also included the transactions in his block that grant him the block reward and the mining fees.
But why are all the other miners including Abdullah’s new block in their personal ledger copies if it gives him the block rewards and fees and doesn’t benefit them?
Well, lets go back to the idea of rational self interest - all the miners are random people who don’t know each other’s identities, spread all over the world.
If each miner decides not to include Abdullah’s block and instead they just choose to keep working on their own candidate blocks, then we once again run into a situation in which everybody has different ledgers. There is no consistency in the ledger and therefore the payment system has no value. This would render everybody’s investment in mining equipment and bitcoin a waste, so the thing that makes the most financial sense for each miner is to follow the rules so that the overall payment system has value.
In this case, the rule that miners need to follow is this - “if some other miner sends you a valid candidate block (ie. a block that has valid transactions and a block header hash that satisfies the difficulty criteria of the mining puzzle), then add it to your local copy of the ledger immediately”. If everybody follows this rule, then everybody should technically have the same ledger!
But what happens if two miners come up with a valid block at the same time? It is possible that Abdullah and Celestine both mine valid blocks at the exact same time. When they send their blocks out to the network, let us assume that Abdullah’s block reaches Beelzebub before Celestine’s does and Celestine’s block reaches Dharmesh before Abdullah’s does (maybe because of geographical proximity between their computers).
We can visualize this situation with the following diagram:
At this point, here is how each node/miner in the network has recorded Block 20 in their individual ledgers. As you can see, Abdullah and Beelzebub have recorded the same block, which has a hash of 0xabcd, but Celestine and Dharmesh have recorded a different block at the same height.
Both the blocks have the same previous block hash (we will come to this in a second), but they have different transactions and different nonces. Although these blocks are different, they are both valid according to the rules set by the Bitcoin program. When anybody computes the value of the block header hash, they will be able to confirm that it meets the difficulty criteria.
Nonetheless, we have a problem - we have two different versions of the ledger right now. This is called a fork in the ledger - there are two different versions! Which version of the ledger is correct? In Abdullah and Beelzebub’s version of the ledger, some transactions may have taken place in block 20 which have not been included in Dharmesh and Celestine’s blocks. So which copy of the ledger should be believed?
Bitcoin solves this problem by giving another rule: “always believe the version of the ledger which has the highest Block Height”. The reason behind this is simple: it is very difficult to generate a block that solves the mining puzzle, so if a version of the ledger has more blocks, that means more work has gone into generating that version of the ledger. That implies that that version of the ledger has the most public support, since it took the most effort to create.
Therefore, to avoid any confusion, Bitcoin instructs miners to always support the ledger which has the most blocks - ie. the version which has the most work behind it. This is why the consensus mechanism in Bitcoin is called proof-of-work.
Anyway, let’s come back to our example. Currently, Abdullah and Beelzebub have one fork of the ledger while Celestine and Dharmesh have another. Despite this incongruity, each miner is still trying to build a candidate block to add to their own fork of the ledger. This is because all of them want the block reward and fees, so they have wasted no time in using their hash power to find the next solution to the mining puzzle.
Imagine now that Dharmesh is the lucky one who finds a valid solution first. The first thing he does is send his block to all the other miners. The other miners have to independently verify the block using the following criteria:
Does the block have a valid previous block hash?
When you hash all of the transactions in the given block, does the resulting transaction hash tally up with the transaction hash given in the block header?
Are all the other fields in the block header correct?
When you hash the block header, do you get a hash which satisfies the difficulty criteria?
Remember, the miners have all the information they need to verify this block. Even though Dharmesh’s new block includes a previous block hash that isn’t present in Abdullah and Beelzebub’s fork of the ledger, Abdullah and Beelzebub still have the data pertaining to that previous block. Basically this means that while Celestine’s new block for 20 reached Abdullah and Beelzebub after those two already recorded Abdullah’s block for height 20 in their ledgers, Celestine’s block for height 20 did still eventually reach them.
So all the miners have the information they need to verify Dharmesh’s latest block for height 21. See the diagram below.
As you can see, Dharmesh has now found a block for height 21, which makes his fork of the ledger the longest out of everybody’s. When the other miners see this, they immediately accept his version of the ledger and start working on candidate blocks for height 22 on top of Dharmesh’s block 21.
In the case of Celestine and Dharmesh, adding block 21 is easy because their version of the ledger contains the same block 20 which is referenced in block 21’s header. But in the case of Abdullah and Beelzebub, they need to replace the block 20 which they had recorded in their ledgers with the block 20 used by Dharmesh. This is called a reorganization of the ledger - because there were conflicting copies of the ledger at a given block height, some miners had to reorganize their ledgers once a certain fork of the ledger became the longest.
We will shortly do some Q&A about reorganization and other concepts, but let us quickly talk about the previous block hash field in the block header. Why is it necessary to include this?
Imagine Beelzebub wants to start playing tricks again by altering his historical ledger and trying to get away with it. Say for example that Beelzebub made a transaction that was confirmed in Block Height 18. In this transaction, Beelzebub paid 20 bitcoin to Dharmesh.
Now let’s say that Beelzebub wants to convince a new Bitcoin user - we will call her Edith - that he never actually spent those 20 coins and that he still has them. One way he might try to do this is to send Edith some alternate version of the ledger in which that transaction never took place.
In Beelzebub’s malicious ledger, he has omitted his transaction from Block 18. However, when Edith independently tallies up Beelzebub’s block 18 header, she will get a different transaction hash since that one transaction has been omitted. And because the transaction hash is different, the block header itself has totally changed! This new block header hash probably doesn’t even satisfy the difficulty criteria. And because the block header hash in block 18 has changed, the hash of block 19 will also change, because the block 19 header has a field for previous block hash! Just like the change in block 18 header changed the block 19 header, the change in block 19 header will percolate all the way through to the latest block.
So basically when Edith is presented with Beelzebub’s malicious ledger copy, all she has to do is verify herself whether Beelzebub’s copy of the ledger is actually mathematically correct. She doesn’t need to trust Beelzebub or anybody else, she can simply go through his ledger and do her own hashes to make sure all the numbers add up properly. At some point while traversing Beelzebub’s ledger, she will notice that the hashes don’t add up and conform to the rules. She will be able to compare Beelzebub’s version of the ledger with the ledger copies of the other, honest nodes in the network.
Since Beelzebub has changed things in a given block, the header of that block has changed, and the headers of all subsequent blocks have also changed. It has become very obvious that he is trying to cheat and present a maliciously edited version of the ledger.
This is the benefit of including the previous block hash in the block header. It becomes possible to create a vertical, continuous, chronological chain of blocks that are inextricably linked to each other. The most minor of changes in any of the blocks in the chain will cause the whole chain’s block header hashes to go out of sync! Its like a mathematical forensic study - the smallest tampering with the transactions or blocks will become immediately apparent to any honest node or miner.
This is why hashes are useful in Bitcoin - it is also why the ledger in Bitcoin is called the blockchain! It is literally a group of blocks which are chained together using their hashes!
And if you think about it, in order to solve the mining puzzle, what are miners doing? They are trying to create their own valid blocks, and when somebody else finds a valid block before them, they are double checking the block. If everything checks out, they add the block to their ledger, otherwise they discard it. In this way, the miners are individually verifying each transaction and upholding the overall integrity of the ledger history because they assume the other rational parties in the system are doing the same. So in Bitcoin, the miners and nodes are the ones who check and process all transactions. And because the transactions are all grouped in blocks which make reference to the preceding block’s hash, it is very easy to see if even one bit in one transaction has been tampered with!
Summary and Conclusion
Amazing everybody!! You got through one of the most complex but interesting concepts to emerge in the 21st century! Here is another piece of eye candy as a reward for making it this far.
Lets just take a moment to recap everything that we learned so far (with a few little clarifications):
Bitcoin is a computer program which has the objective of creating a payment system which does not rely on any central trusted party
Computers which run the Bitcoin program are called nodes
Each node maintains its own personal copy of the transaction ledger, known as the blockchain
Transactions in the Bitcoin payment system can be verified by anybody through the use of cryptographic digital signatures
Before transactions are added into the ledger, they are grouped together in structures called blocks
Anybody (it could be through a website or mobile app, not just a node or miner) can create a bitcoin transaction, and send it out to the network
All the nodes in the Bitcoin network are constantly talking to each other and telling each other about any new transactions they hear about
Some of the nodes in the network continually attempt to append a block of transactions to the ledger by solving a computationally expensive mining puzzle (basically doing lots of hashing operations in the hope of getting a rare one starting with many 0s)
The nodes which attempt this are called miners. Not all nodes are miners. Some nodes just listen to the network for new transactions and blocks. They keep a complete copy of the ledger so that they can independently verify all transactions and don’t need to trust anybody to see what is a valid confirmed transaction in the ledger and what isn’t. This process of just verifying the blockchain is relatively cheap and easy to carry out, so there are many non-mining nodes in the Bitcoin network in addition to miners.
In contrast, mining is very computationally heavy work that requires expensive specialized computers that can perform millions of hashes a second. Miners purchase these computers because there is a monetary incentive promised to successful miners. This incentive takes the form of a ‘block reward’ of newly minted bitcoin which goes to one lucky miner. Additionally, that lucky miner is also able to claim all the transaction fees embedded in the transactions included in the block they mine.
In order to win the block reward and get the mining fees, miners have to complete a mining puzzle which involves finding a block header hash with a large number of leading 0s.
When a lucky miner (statistically likely to be the miner with the greatest hash power) finds the solution to the mining puzzle, they broadcast this solution to all of the other nodes and miners.
As part of the solution, the lucky miner sends the list of transactions he wishes to include in the block (including the minting transactions which grant him the block reward and mining fees). He also sends a block header, which is a list of different fields including a previous block hash, block height, timestamp, transactions hash, difficulty, and a nonce.
Upon receiving this information from the lucky miner, the other miners and nodes are able to quickly and independently run the hashes and signature verifications for themselves to see whether the given candidate block truly satisfies the Bitcoin program’s criteria.
If the miners and nodes verify that the given block is truly a valid block, they each independently add the given block to their local copy of the ledger (or blockchain). They do this because of a game theoretical imperative to follow the rules of the Bitcoin program.
Next, the miners immediately start working to try and generate a new block of transactions to add to the chain.
If all of that is clear, you’ve done it! You’ve understood Bitcoin! This is actually a massive achievement so take a moment to just congratulate yourself and soak it in. Isn’t this an incredible system? It is truly one of the most creative and interesting ideas I have come across in my life. Anyway, lets see if we can square off what we learned about Bitcoin’s mechanism with Satoshi’s original objective.
Looking at the system we described above, we can say the following:
Bitcoin is a payment system based off of a free, publicly accessible computer program. Anybody can make and receive payments using the native currency of the system, called bitcoin.
The ledger of accounts in Bitcoin is called a blockchain. Anybody who installs the Bitcoin program can get a copy of the blockchain by talking to all the other computers who are also running the program. Each person’s copy of the ledger could be different, but due to the economic incentives baked into this system, it is very likely that the vast majority of people have a consistent version of the ledger.
Going a step further, anybody is able to verify the integrity of the blockchain by independently computing and checking all of the hashes, transactions, and signatures that make up this data structure
In this way, Bitcoin is able to create a fully functional, trustable payment system which doesn’t need a central trusted intermediary! This is a remarkable feat, made possible through an extremely elegant marriage of cryptography, peer-to-peer technologies, and game theory. Bitcoin represents a completely new paradigm for collectively agreeing on some important system of record without needing to establish an authority or gatekeeper. This could serve as the basis for radically different systems for organizing resources (a new banking system for example).
This is why I believe that Satoshi Nakamoto deserves the Turing Prize for computing and the Nobel Prize for Economics.
I hope that you agree with me! In the next section, I have written some answers to common questions that readers might have when going through this post. But first, to make you feel good about yourself, here is a list of all the concepts you truly understand now!
What is a blockchain?
What is proof of work?
What is hashing?
What is a digital signature?
What is bitcoin mining?
How do you achieve decentralized consensus?
Great job everybody, and thank you for reading! We hope you learned something interesting and will come back to check out our future articles!
7. Bitcoin and Blockchain FAQS:
Who sets the difficulty in the block header? Can anybody just choose a difficulty level on their own?
Excellent question. The difficulty level in Bitcoin can be calculated using a simple formula provided by the Bitcoin program rules. This formula basically checks the timestamp in each block (remember, the block header contains a time stamp) and increases or decreases the difficulty level so that the difference between the time stamps averages out at 10 mins (so that there are 10 mins between blocks).
This means that as more and more miners join the network and contribute more to the network hashpower, the time between blocks will get shorter. However, when the difficulty formula detects that this is happening, it increases the difficulty so that miners take longer time to find the right solution to the puzzle. The reason the time between blocks is intended to be 10 minutes is because if the time was shorter, the chances of people coming up with equally valid blocks at the exact same time would be higher. This would create many forks in the blockchain and lead to excess reorganization.
Why is blockchain reorganization undesirable? How can it be avoided?
In our example, the blockchain was reorganized at height 20. This meant that some transactions that happened in Abdullah and Beelzebub’s fork of the ledger in block 20 were not included in what would become the main chain (the longer blockchain produced by Dharmesh).
This is not a good thing for any payment system. You don’t want transactions to be rolled back suddenly. For this reason, people using bitcoin are advised to wait for at least 6 blocks after their transaction is confirmed in the blockchain to actually assume their transaction is final.
Say for instance I am selling you a copy of Microsoft Word for 1 bitcoin. You create a bitcoin transaction giving me one bitcoin and send it out to the network of nodes and miners. One of the miners picks it up and includes it in a valid block. Even if all the nodes and miners include this block - and by extension, our transaction - into their ledgers, I still shouldn’t allow you to start your download. This is because the blockchain may get reorganized and the transaction which credits one of your bitcoins to my account may not be included in the new version of the blockchain.
However, if I wait for 6 blocks to get confirmed on top of the block in which our transaction was first included, then the chances of this transaction getting affected by a reorganization are very low. Imagine our transaction is confirmed in block #100. As soon as block 100 is confirmed, all the rational profit-seekers will immediately start trying to build on top of block 100 to create block 101 and claim the block reward for block 101. When the blockchain reaches height 106, everybody will be working on block 107. So for our transaction to be affected, somebody needs to find a solution to block 100, 101, 102, 103, 104, 105, 106, AND block 107 before any other miner finds a solution to block 107. The chances of this happening are almost 0! The party that wishes to reorganize the chain has to have multiple times more hash power than everybody else out together.
Is that possible? If one party gets too much hash power, wouldn’t that break the system? What about quantum computing? Do quantum computers pose a threat to this system?
Again, excellent questions. The answer is yes - if a given entity gains more than 51% of the hash power, then the security of the Bitcoin blockchain can theoretically be lost.
If a party had 51% of the hash power and was dishonest, they could theoretically start trying to reorganize the chain from any point in its history and they would likely succeed in the long run because they can find valid solutions to the mining puzzle faster than everybody else can.
Nonetheless, doing this is much easier said than done. Firstly, it would require a herculean investment in mining computers and electricity. Secondly, this reorganization would take a long time to happen, as the other honest miners would presumably keep using their computing resources to extend the length of the honest, consensus chain. Thirdly, there would be no economic incentive to this act.
By crossing the 51% threshold, any miner would be theoretically making Bitcoin’s consensus mechanism prone to abuse. This would shake up faith in the whole system and tank the value of bitcoin and bitcoin mining equipment. Therefore, this would be a highly irrational and self-destructive act for anybody to do. They would basically be investing lots of time and money to destroy Bitcoin for no gain to themselves.
In the past, some miners did approach 51% hash power. However, they willingly pulled back on their hash power to ensure the continued safety and integrity of the Bitcoin system.
As for quantum computing, it could pose a risk to Bitcoin. If somebody got hold of a functional and reliable quantum computer, they would probably be able to generate hashes very quickly. They would probably even be able to reverse engineer hashes and signatures. This would not only invalidate the security of Bitcoin, it would also invalidate the security of every other computer program we use today. The cryptography which protects our bank accounts and nuclear bunkers would all be at risk.
Luckily, cryptographers have been able to develop quantum-resistant hash-functions and quantum-resistant signature and encryption schemes (encryption was not covered in this piece but basically encryption allows you to jumble some data or message so that only a party with a given key can unjumble and read it). In short, Bitcoin and other cryptocurrencies have a roadmap to protect themselves in case quantum computers come to market sooner than expected.
How would Bitcoin make this upgrade to become quantum-resistant? Aren’t the rules of Bitcoin set in stone by the Program?
Bitcoin is an open source program. This means that anybody can download and change the rules however they like. However, there is no point in having your own personal version of Bitcoin that nobody else values.
Imagine your bank database was open-source. Anybody could download it and change the balances. But if you came and showed me your homemade bank database which made you a billionaire, it would have no meaning to me. I would still be able to follow the version of the database which I trust - the one which is maintained by the bank.
Similarly, anybody is free to create new versions of Bitcoin. Somebody might decide to give themselves millions of Bitcoin, but that person would probably be unsuccessful in convincing the rest of the network to adopt their version. It would be clear if somebody was using a version of Bitcoin that was different from the majority.
On the other hand, an ingenious young programmer might come up with a way to make Bitcoin more secure or more efficient. If this person’s idea was seen to have value by all the other miners and nodes, they could audit her code and elect to introduce it into their own personal versions of the Bitcoin program. There are two mechanisms to coordinate this software upgrade - they are called hard forks and soft forks.
We won’t go into the details, but all you need to know is that anybody can suggest a change to Bitcoin. If the majority of nodes and miners find merit in the idea, the system can be upgraded. There have been hundreds of these kinds of upgrades since Bitcoin was launched. This meritocratic, free way of maintaining the software is one reason why so many talented programmers flock to Bitcoin and other cryptocurrencies.
Since we are on the topic of cryptocurrencies, what is Ethereum?
I don’t want to get into that in this piece. I will just leave you with a thought experiment. In Bitcoin, everybody has a copy of a ledger which contains information about account balances and transactions between parties.
What if the ledger contained more information? What if the ledger could contain an electronic version of your house title? Or electronic versions of stocks in your company? What if you had the freedom to fix the rules for how these stocks and titles could be used and traded?
Ethereum was designed to see what would happen if Bitcoin’s decentralized payment system could be extended to serve as a decentralized database for any kind of application, not just a payments system. Ethereum, and other projects which aim to extend upon the ideas introduced by Bitcoin, are indeed very interesting but they are out of scope of this piece.
What about blockchain technology as a whole? I have heard of blockchains being used for everything under the sun?
A blockchain is simply a data structure. In the case of Bitcoin, everybody keeps their own record of this data structure so that they can independently verify all transactions without needing to trust anybody. There is no trust in Bitcoin because there are no real world identities here - only pseudonymous folks using public keys on the internet. It is necessary for everybody to keep their own record of the ledger even though it involves lots of duplication of effort because nobody wants to have to trust a stranger.
In other types of applications which involve trusted parties using their real identities and working under a legal system, a blockchain may not be necessary. In fact, it may even be counterproductive as it slows things down and introduces a lot of extra complexity. Having said that, there are many different kinds of blockchains and each has their own unique properties. Some of them might have really clever real-world applications, but in my experience 99% of the projects that claim to use blockchain technology would be better off using a SQL database.
8. Glossary:
Block: In Bitcoin, transactions are grouped into structures called blocks. Besides containing a number of transactions, a block also contains a component called a block header.
Blockchain: In Bitcoin, the ‘blockchain’ refers to the ledger of transactions that has been organized into blocks that build on top of each other in a continuous, sequential order.
Block header: A block header is just a list of a few fields: previous block hash, block height, time stamp, transaction hash, difficulty, and nonce. Along with the transactions, the block header is what makes up a bitcoin block.
Block height: The block height of a Bitcoin block refers to its numerical order in the sequence of blocks in the blockchain. The very first Bitcoin block had a height of 0, and each subsequent block has had a higher height. Currently, the block height in Bitcoin is 648557.
Block reward: The block reward is a prize of newly minted bitcoin which gets created and handed over to the miner who manages to create a valid new block. Currently, the block reward for miners is 6.25 bitcoin per block, but eventually the block reward will go to 0 and the number of all bitcoin in circulation will cap out at 21 million (currently at around 17 million). The block reward is one part (along with mining fees) of the economic incentive for miners to keep validating blocks and transactions in the Bitcoin network.
Candidate block: When a miner attempts to solve the mining puzzle, they repeatedly create new blocks in the hope that they are able to crack the puzzle. The blocks which miners create in this attempt are known as candidate blocks.
Difficulty: In simplified terms, the difficulty of a block indicates how many 0s the block header hash needs to begin with in order to satisfy the mining puzzle of the Bitcoin program. Since each digit in a hash has a 50% chance of being 0 and 50% chance of being 1, the higher the difficulty, the more improbable it is that any miner discovers a valid solution to the mining puzzle. In Bitcoin, the difficulty level is dynamically determined by the total hash power on the network. As the collective hash/second capacity of miners goes up or down, the difficulty in Bitcoin goes up or down so that the average time between blocks stays at ~10 minutes.
Digital signature: A digital signature is the output which gets produced when somebody puts a certain message and private key into a digital signature generation function. This output - the signature - can be validated using a signature verification function. Using the signature, the message, and the public key which corresponds to the signer’s private key, the verification function can tell you whether the holder of that private key really signed that exact message or not.
Hashing: Hashing refers to the act of putting some input into a hash function and producing an output called a hash. As long as the input doesn’t get changed, the hash will never change. Therefore, hashing gives us a useful way of keeping track of the integrity of some data by constantly checking its hash to see whether it has been tampered with.
Miner: Any computer that attempts to solve the mining puzzle is called a miner. Miners are profit-seeking parties that attempt to solve the mining puzzle in search of the lucrative block rewards and mining fees offered to miners. Today, miners are sophisticated entities that consume vast amount of electricity and computing power in support of their goal.
Mining puzzle: The mining puzzle in Bitcoin is a contest based on generating hashes of block headers. Only block headers that begin with an improbably low number of zeros satisfy the mining puzzle. Generating these block headers is so unlikely that it requires lots of time and computing power to solve the mining puzzle. Solving the mining puzzle yields a block reward.
Node: Any computer that keeps a running copy of the Bitcoin program is called a node. Like miners, nodes store a record of the entire ledger, including all the blocks and transactions. This allows them to verify any transaction for themselves without trusting any third party. Unlike miners, nodes do not attempt to solve the computationally expensive mining puzzle.
Nonce: The nonce is a number that is part of the block header. Miners use the nonce to change the input each time they need to make a new candidate block to solve the mining puzzle. When a miner hashes a candidate block header and gets an unsatisfactory output, he can increase the nonce by 1 and try again. This difference in the input gives the new block header hash a new, equal chance to satisfy the difficulty criteria of the mining puzzle. There is always some nonce value that would give a miner’s candidate block the right number of leading 0s to solve the difficulty. This is what all the miner’s are each looking for, and the only way to look is to keep hashing a block header with different nonce values until you strike gold (changing the nonce is way faster and easier than changing any other part of the block header).
Private key: It is a special number generated as part of a cryptographic keypair. It always comes with an associated public key. The private key can be used like a password that proves that you are the owner of a certain public key.
Public key: It is a special number generated as part of a cryptographic keypair. It always comes with an associated private key. In Bitcoin, the public key is your main public identifier. You can give your public key to anybody, and they can send you bitcoin to your public key. However, in order for you to spend bitcoin associated with your public key, you need to prove that you own the corresponding private key by generating a valid signature in your transaction.
Transaction hash: In a given block, all the transactions can be hashed together to generate a single hash called the transaction hash. This is useful for checking whether somebody has tampered with the transactions in a block. If somebody has changed the transactions in a block, the transaction hash generated by hashing the tampered transactions won’t match the transaction hash of the untampered transactions. Keeping a hash of all the transactions is a good way to check that nothing in those transactions has changed. The real name for a transaction hash is a Merkle Root Hash.
Further Reading:
In my opinion, the best resources on cryptocurrencies and Bitcoin are:
Free Bitcoin Textbook by Princeton University Professors
The Age of Cryptocurrencies by Michael Casey and Paul Vigna
Acknowledgements:
I would like to thank Rahul, Jehan Karanjia, and Divraj Jain for helping me fine tune this piece. And if you seriously made it this far as a reader, then I am stunned and grateful. I hope you enjoyed the read.








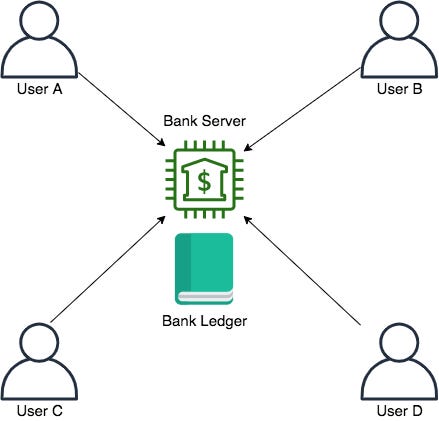
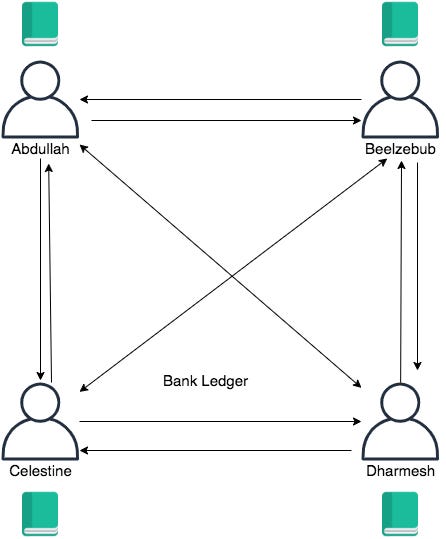
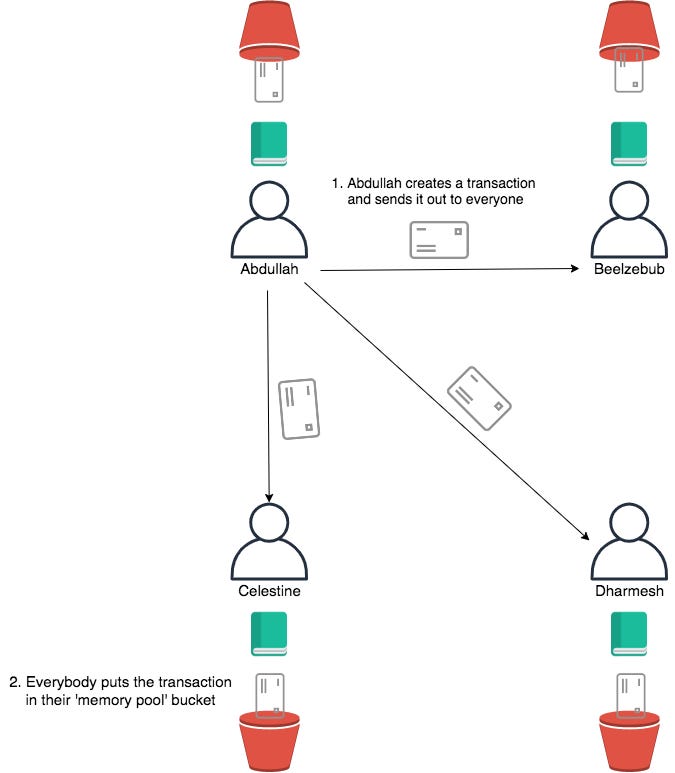
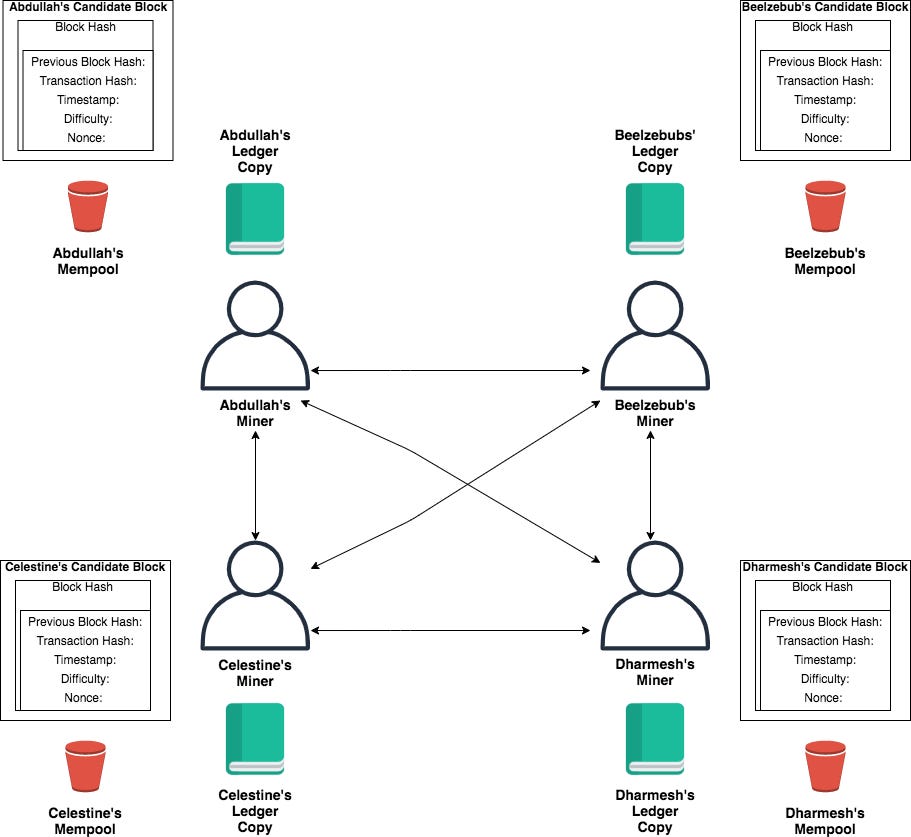
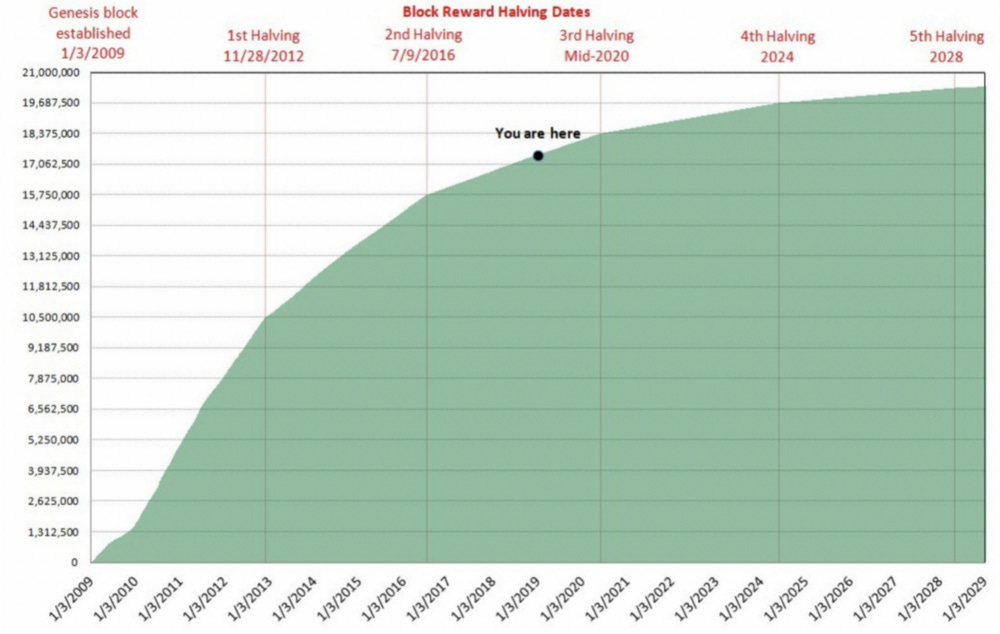
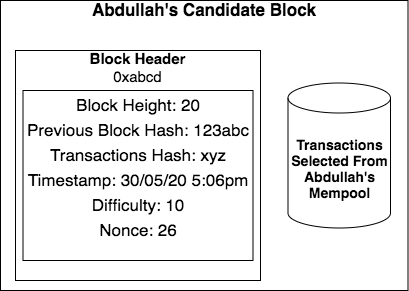
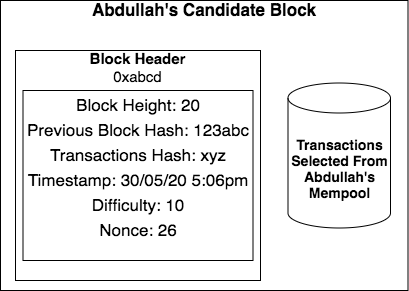





Great article 👏. Reads like a nice story from beginning to end.
Great article. Thank you so much Aaryaman.